Goniometrie

Vzhled přesunout do postranního panelu skrýt

Goniometrie (z řeckého gónia = úhel a metró = měřím) je oblast matematiky, která se zabývá goniometrickými funkcemi jako sinus, kosinus, tangens a kotangens. Její součástí je také trigonometrie, která se věnuje praktickému užití těchto funkcí při řešení různých úloh o trojúhelnících.

Historie goniometrie

Základy goniometrie položili již Egypťané a Babyloňané. Po Alexandrově výpravě do Asie převzali tyto znalosti spolu s dělením úhlu na 360° Řekové. Hlavním bodem zájmu babylonských a řeckých vědců byl podoobor dnešní goniometrie, trigonometrie, zvláště pak trigonometrie sférická (trigonometrie útvarů na kulové ploše). Jejím průkopníkem se stal Aristarchos ze Samu, který studoval vzdálenosti Slunce a Měsíce od Země.

Dále v budování goniometrie pokračovali vědci z Indie a Arábie, kteří věnovali úsilí spíše kalkulativním problémům a aritmetickým algoritmům. Indové zavedli funkce, které se později ustálily pod jmény sinus a kosinus (kosinus znamenal sinus doplňku do 90°).

Dnes používané termíny pro tangens (tečna), kotangens (doplněk do tečny), sekans (sečna) a kosekans se poprvé objevily až během 16. a 17. století v Evropě. V tomto období se utřiďovaly všechny doposud známé poznatky a goniometrické funkce se začaly používat pro popis periodických dějů.

Užití goniometrie

V současnosti poznatky z goniometrie uplatňuje velké množství oborů, zejména pak astronomie, geodézie a satelitní navigační systémy k určování vzájemných pozic dvou bodů (tato technika se nazývá triangulace). Dále goniometrii využívá hudební teorie, akustika, optika, elektronika, biologie, statistika, lékařská diagnostika (ultrazvuk a tomografie), chemie, kryptologie, seismologie, oceánografie, meteorologie, fonetika, architektura, ekonomie, krystalografie, počítačová grafika a mnoho fyzikálních věd.

Goniometrické funkce

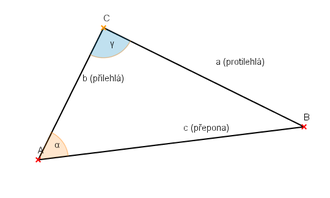Pravoúhlý trojúhelník s pravým úhlem γ při vrcholu C. Přilehlá a protilehlá odvěsna se vztahují k úhlu α

Hodnoty goniometrických funkcí v pravoúhlém trojúhelníku

Sinus α {\displaystyle \alpha } $\alpha$ je poměr délky odvěsny protilehlé tomuto úhlu a délky přepony.

sin ⁡ α = a c {\displaystyle \sin \alpha ={\frac {a}{c}}}

\sin \alpha ={\frac {a}{c}}

Kosinus α {\displaystyle \alpha } $\alpha$ je poměr délky odvěsny přilehlé tomuto úhlu a délky přepony.

cos ⁡ α = b c {\displaystyle \cos \alpha ={\frac {b}{c}}}

\cos \alpha ={\frac {b}{c}}

Tangens α {\displaystyle \alpha } $\alpha$ je poměr délek odvěsny protilehlé tomuto úhlu a délky odvěsny k němu přilehlé.

tg α = a b = sin ⁡ α cos ⁡ α {\displaystyle {\textrm {tg}}\,\alpha ={\frac {a}{b}}={\frac {\sin \alpha }{\cos \alpha }}}

{\textrm {tg}}\,\alpha ={\frac {a}{b}}={\frac {\sin \alpha }{\cos \alpha }}

Kotangens α {\displaystyle \alpha } $\alpha$ je poměr délek odvěsny přilehlé tomuto úhlu a délky odvěsny k němu protilehlé.

cotg α = b a = cos ⁡ α sin ⁡ α {\displaystyle {\textrm {cotg}}\,\alpha ={\frac {b}{a}}={\frac {\cos \alpha }{\sin \alpha }}}

{\textrm {cotg}}\,\alpha ={\frac {b}{a}}={\frac {\cos \alpha }{\sin \alpha }}

Sekans α {\displaystyle \alpha } $\alpha$ je poměr délky přepony a délky odvěsny přilehlé tomuto úhlu.

sec ⁡ α = c b = 1 cos ⁡ α {\displaystyle \sec \alpha ={\frac {c}{b}}={\frac {1}{\cos \alpha }}}

\sec \alpha ={\frac {c}{b}}={\frac {1}{\cos \alpha }}

Kosekans α {\displaystyle \alpha } $\alpha$ je poměr délky přepony a délky odvěsny protilehlé tomuto úhlu.

cosec α = c a = 1 sin ⁡ α {\displaystyle {\textrm {cosec}}\,\alpha ={\frac {c}{a}}={\frac {1}{\sin \alpha }}}

{\textrm {cosec}}\,\alpha ={\frac {c}{a}}={\frac {1}{\sin \alpha }}

Související články

Externí odkazy

Učebnice goniometrie a trigonometrie
Trigonometry (anglicky) - v angličtině se goniometrie a trigonometrie souhrnně označuje jako trigonometry

NKC: ph120582
PSH: 7312

Portály: Matematika